I’ve been doing a lot of maths recently on Khan Academy which has been great, and I’ll write more about this soon and it has been particularly interesting re-learning some maths after having done some coding for a few years. I’m starting to see how useful all the maths I learnt at college is, and also starting to realise what half the code I have written/copied actually does. As I’ve been sorting out my website I’ve been digging out lots of old experiments so I decided to pick apart one such experiment to see if I can really understand what is going on.

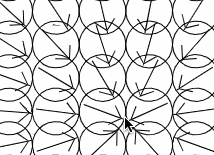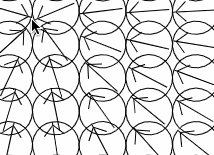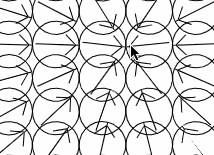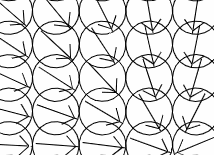
The satisfying wobbly dots thing above is about 5 years old now. I got to this point after following a few tutorials on the wonderful Coding Math YouTube channel. The narrator does a good job of explaining the Maths as he goes, but not quite in the detail I now want. Evidentally it was somehow rotating each dot to the direction of where the mouse is located, that much is clear.
First I replaced the dots with arrows which was how it was originally created. I also thought I had corrected the atan2 function by putting the x before the y which confused things even further:
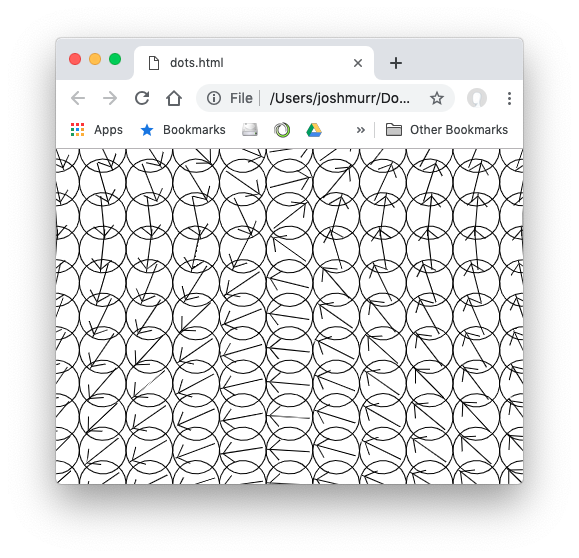
All the arrows are supposed to be pointing at the mouse location, which, when I swapped the x and y back around again, it did work (ie. Math.atan2(y,x)):
I also noticed how slow it could get if I started resizing the window or playing with the rows and cols which should quite simply change the number of arrows on the screen. Changing the color of one of the arrows was making no sense at all either, as the ID’s they should be were not working. So I added an ID to each arrow and wrote it on the screen:
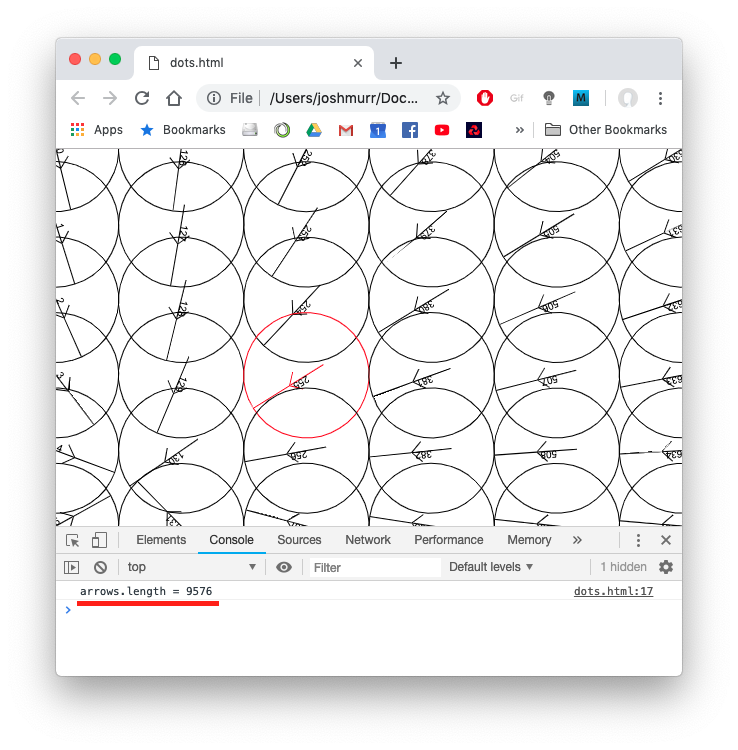
Something wasn’t right! Naturally it was an issue up in the for loops which filled the arrows array with all the arrows. I sorted that out and also changed how each arrow is placed on screen with this snippet
xloc = (ii * (width/cols)) + ((width/cols)/2);
yloc = (i * (height/rows)) + ((height/rows)/2);
arrows.push(new arrow(xloc,yloc, i+ii));
I’m sure there is a better way of doing that, but everything now seemed to be sorted:
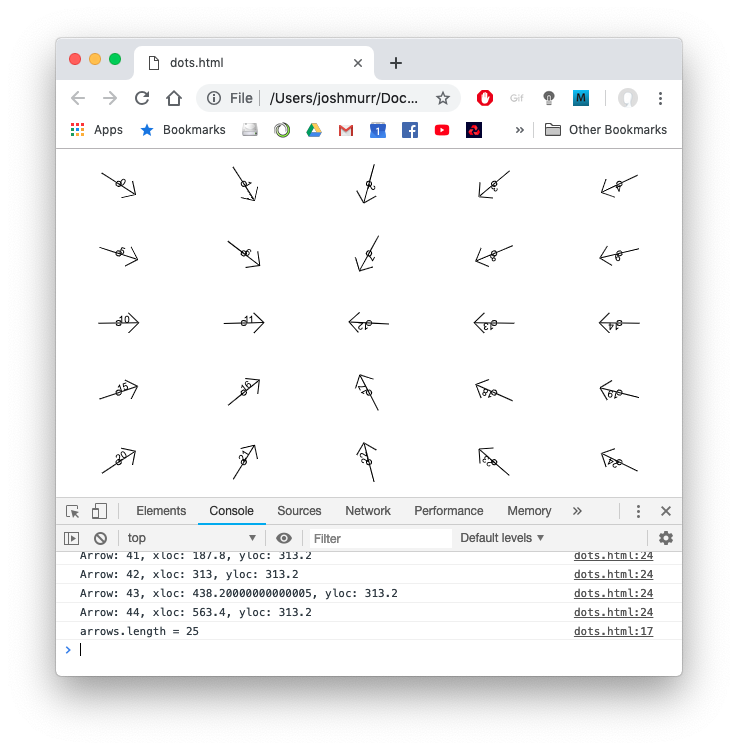
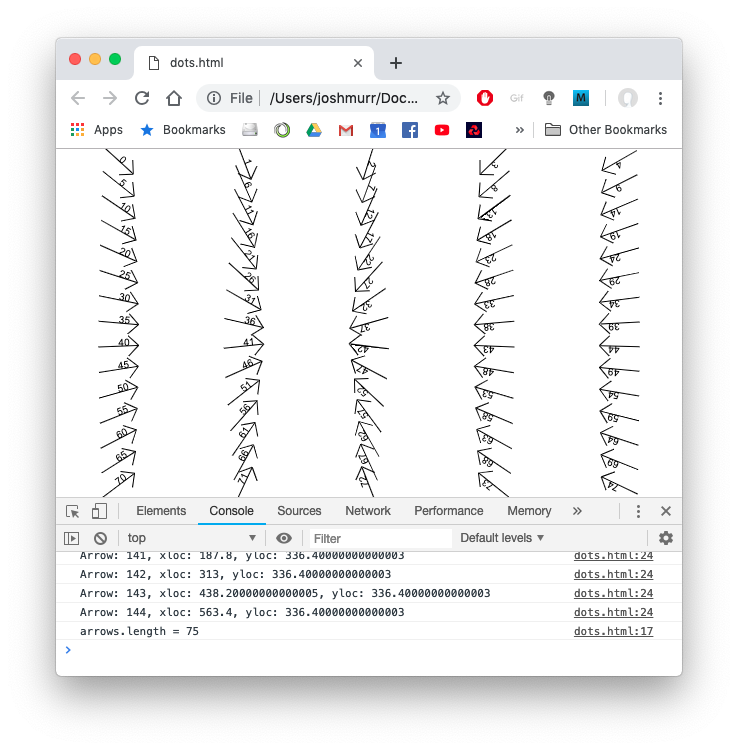
Now I could start doing some maths! I played with JSBin a little to get to grips with the atan2 function which clearly was doing all the work here:
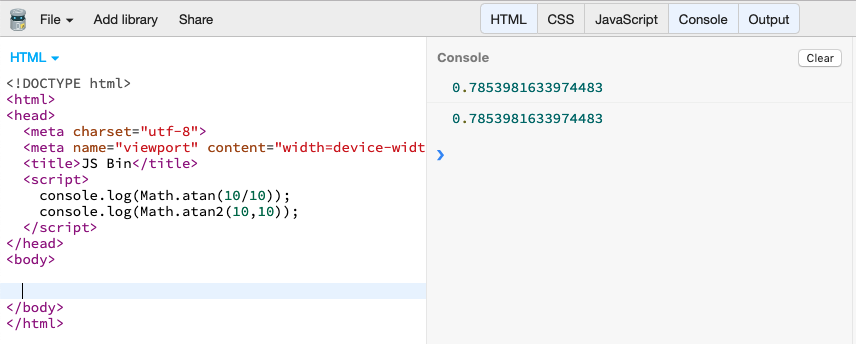
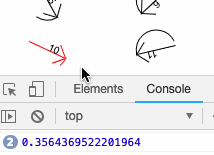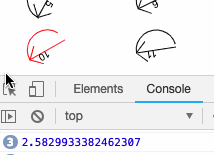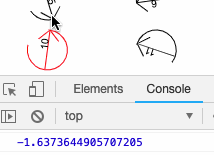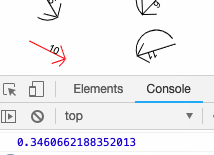
Atan2 does quite simply return the ArcTangent of two given co-ordinates x and y but given to the function as so: Math.atan2(y,x). This is useful for finding the angle between a point on the canvas and the mouse location as if you take the change in x as mousex - x1 and the change in y as mouseY - y1 the result is the angle in radians from the point (x1, y1) pointing to to (mouseX, mouseY). I had to work this out using some arbitrary co-ordinates as examples, and also logging the co-ordinates of the mouse, a given arrow and it’s angle to the console.
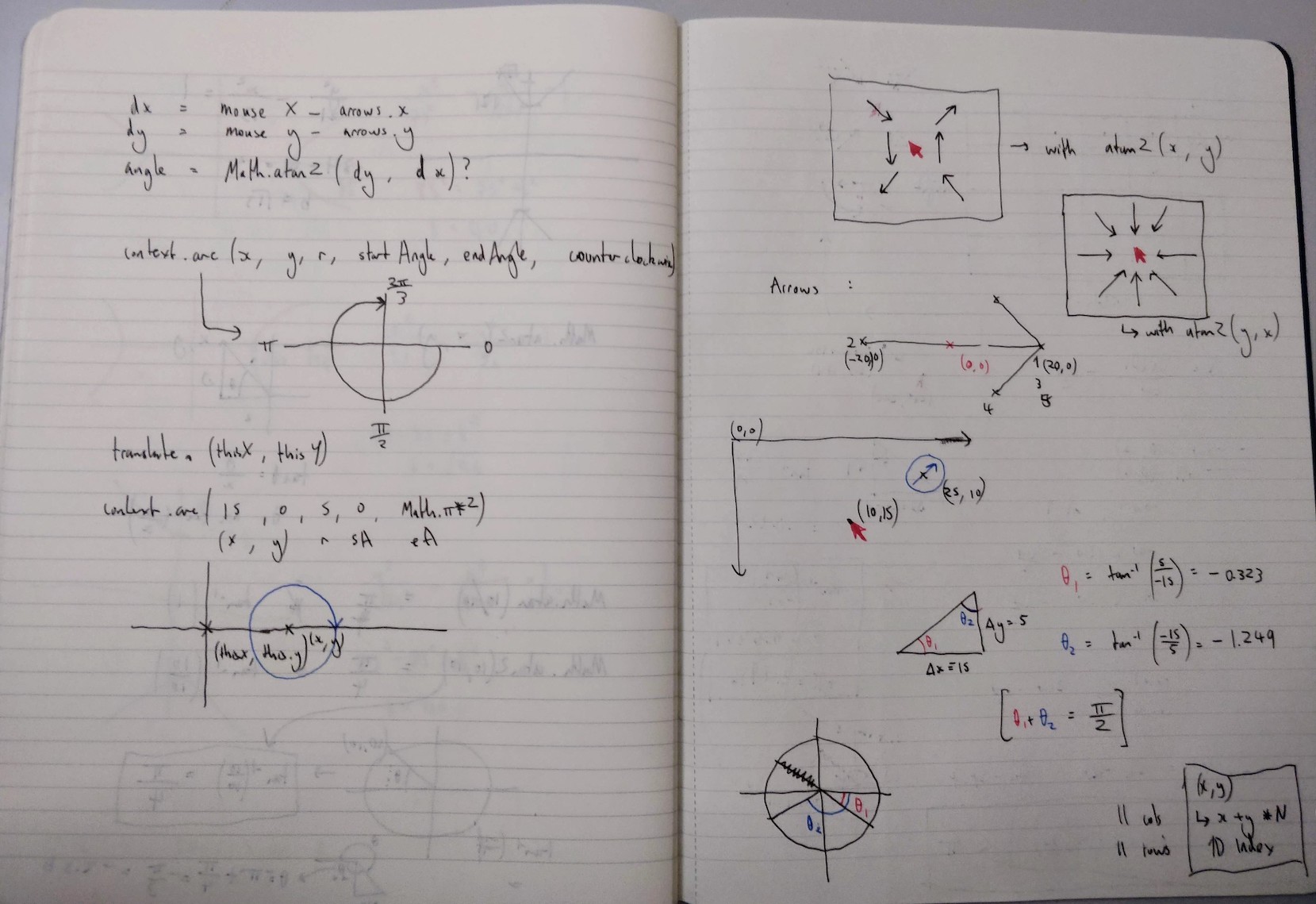

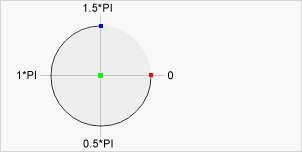
I also found in my scribbling that atan2 only returns an angle between -π and π which I later confirmed on Wikipedia:

It still took my a while to get my head around how simply adding context.rotate(this.angle); was enough to rotate every item drawn to the direction of the mouse. It is down (I think) to the way that the javascript circle is drawn (the same as the unit circle) so it maps to the co-ordinates of the screen (where (0,0) is the top-left corner). The fact that -π < atan2 < π is essentially irrelevant to the maths as it produces the same results as if you were working it out on paper.
So finally I could change it back to the original circles happy in the knowledge I truly understand this simple little trick. 3 hours well spent…

It actually was 3 hours well spent I think. At the very least it’s satisfying to truly understand something which you once took for granted. It’s also a nice way to keep language I’m not really using right now a bit fresher in my memory — it was actually quite nice to be using Javascript again. It’s also giving me faith in my decision to really work on the maths.
I will post the code below, but currently I don’t have everything set up to format code blocks nicely, that’ll change hopefully soon:
window.onload = function() {
var canvas = document.getElementById("canvas"),
context = canvas.getContext("2d"),
width = canvas.width = window.innerWidth,
height = canvas.height = window.innerHeight,
cols = 30,
rows = 20,
arrows = [];
init();
globalRender();
function init(){
for(var i=0; i<rows; i++){
for(var ii=0; ii<cols; ii++){
xloc = (ii * (width/cols)) + ((width/cols)/2);
yloc = (i * (height/rows)) + ((height/rows)/2);
arrows.push(new arrow(xloc,yloc, i+ii));
}
}
}
function globalRender(){
context.clearRect(0,0,width,height);
for(var j=0; j<arrows.length; j++){
arrows[j].render(j);
}
requestAnimationFrame(globalRender);
}
function arrow(x_, y_, id_){
this.x = x_;
this.y = y_;
this.angle = 0;
this.dx, this.dy;
this.id = id_;
this.render = function(id2){
context.save();
context.translate(this.x,this.y);
context.rotate(this.angle);
context.beginPath();
/*context.moveTo(20,0);
context.lineTo(-20,0);
context.moveTo(20,0);
context.lineTo(10,-10);
context.moveTo(20,0);
context.lineTo(10,10);*/
context.arc(15,0,3,0,Math.PI*2);
context.fill();
context.restore();
}
}
document.body.addEventListener("mousemove",function(event){
for(var k=0; k<arrows.length; k++){
arrows[k].dx = event.clientX - arrows[k].x;
arrows[k].dy = event.clientY - arrows[k].y;
arrows[k].angle = Math.atan2(arrows[k].dy,arrows[k].dx);
}
});
};
Josh